P値の収束に関する数学的考察

CADの西村と石橋です。この記事では、数理統計のトピックの中でも、仮説検定における\(P\)値の振る舞いについて考察しようと思います。ただし、著者は数理統計学の専門家ではなく、誤りを見つけられた場合はご指摘いただけると幸いです。

みなさんは、「サンプルサイズが大きければ、統計的仮説検定において有意差を検出しやすい」といった議論を目にしたことはありますでしょうか？例えば統計ライブラリー　サンプルサイズの決め方　 ｜朝倉書店 (asakura.co.jp)のまえがきや、統計的有意性と P 値に関する ASA 声明などで言及されています。

この現象は数学的にどのように説明できるか？と疑問を持ったのですが、枠組みの定式化において苦労する点が多く、「記事にすれば興味をもっていただけるのでは？」と思い至りました。

なのでこの記事では、「対立仮説が正しい場合、サンプルサイズが大きくなれば\(P\)値が0へ収束する」といった形で、定式化し証明をつけることで疑問を解決しようと思います。

※帰無仮説が正しい場合、\(P\)値はサンプルサイズに依らず一様分布に従う確率変数となります。

定義

さて、 ”目標”の中で \(P\)値 や概収束といった概念を使いました。今回採用した定式化や証明の中で大事な部分なので、この定義を改めて振り返っておこうと思います。

定義（ \(P\)値）

最初に統計量 \(T_n\)を次のように定めます：

\(T_n
:= \bar{X}
_n /(\sigma/\sqrt{n})\)

さらに帰無仮説のもとでの \(|T_n |\)の分布の上側確率を \(Q_n\)とあらわすことにします：

\(Q_n(t)
:= p_0 (|T_n| \geq t
), \ t\in \mathbb{R}\)

以上の準備の下で、 この検定における \(P\)値 は次のように定められます:

\(P_n := Q_n(|T_n|)\)

すなわち標本空間の元 \(\omega\)に対して、

\(P_n(\omega)= Q_n(|T_n(\omega)|)= p_0 (|T_n| \geq |T_n(\omega)|).\)

ここで注意として、 \(T_n\)は確率変数であるため、 関数への代入結果である \(P_n\)も確率変数です。 （要するに標本を取ってきて初めて値が確定する。）なお、 \(P\)値 の値の解釈に関する話題は他の文献を参照いただけると幸いです。

p値ってなんだっけ？ #統計学 - Qiita

Amazon.co.jp: 新装改訂版 現代数理統計学 : 竹村 彰通: 本

定義（概収束）

最後に \(P_n\)が（ \(p_{\mu_0}\)に関して） \(0\)に概収束するとは、次が成立するときにいいます：

\(p_{\mu_0} (\{ \omega |
\lim_{n\rightarrow \infty} P_n (\omega) \neq 0\}) = 0.\)

また、このとき \(\lim_{n\rightarrow \infty} P_n =0 \ \text{a.s.}\) などと表記します。 ここで、a.s. は almost sure の略です。

証明の道具

概収束とは何かわかったところで証明に入っていきたいのですが、 その前に道具を2つ準備しておきます。

大数の強法則

\(\bar{X}_{n}\)は \(p_{\mu_0}\)について \(\mu_0\)に概収束する。

中心極限定理

\(\Phi\)を標準正規分布の分布関数とすると、 以下が成り立つ:

\(\lim_{n\rightarrow \infty} \sup_{z\in \mathbb{R}}|F_{T_{n}}(z) - \Phi(z)| = 0\)

ここで

\(F_{T_n}(x)
:=p_0 (T_n \leq x), \quad x\in \mathbb{R}.\)

Remark.

中心極限定理は法則収束（分布関数列の各点収束）で記述されるのが一般的ですが、 法則収束から分布の一様収束を示すのは容易です。証明はAppendixに記載します。

目標の証明

以上で準備ができたので、目標の主張を証明していきます。

まず、大数の強法則より, \(p_{\mu_0}\) に関して、

\(\bar{X}_n\rightarrow \mu_0\quad a.s. \ in\ \Omega\)

ここで、対立仮説が正しいという仮定から \(\mu \neq 0\)であることに注意すれば, \(p_{\mu_0}\)に関して

\(t_n :=|T_n| \rightarrow +\infty \quad a.s.\ in\ \Omega\)

このとき、 \(p_{\mu_0}\)に関して

\(\begin{aligned}
P_n
&= 1 - p_0 (T_n < t_n) + p_0 (T_n < -t_n)\\
&\leq 1 - p_0 (T_n \leq t_n - 1 ) + p_0 (T_n \leq -t_n + 1)\\
&= 1 - F_{T_n}(t_n -1) + F_{T_n}(-t_n +1)\\
&= 1 - \Phi(t_n -1) + \Phi(t_n -1)- F_{T_n}(t_n - 1) + F_{T_n}(-t_n + 1) -\Phi(-t_n + 1)+ \Phi(-t_n + 1)\\
&\leq |1 - \Phi(t_n -1)| + |\Phi(-t_n +1)| + 2\sup_{z\in \mathbb{R}}|F_{T_{n}}(z) - \Phi(z)|
\end{aligned} \)

したがって、 中心極限定理と分布関数の基本的な性質から \(\lim_{n\rightarrow \infty} P_n =0 \ \text{a.s.}\)が示された. 

Appendix

補題

\(\{ F_n \}_n\)を分布関数の列とし、ある分布関数 \(F\)に各点収束しているとする。

このとき、 \(F\)が連続であれば \(\{ F_n \}_n\)は \(F\) に一様収束する。

補題の証明

\(\lim_{x\rightarrow \infty}F(x) = 1,\ \lim_{x\rightarrow -\infty}F(x) = 0\)なので、任意に \(\varepsilon >0\)をとれば、
ある \(a, b \in \mathbb{R}\)が存在して、次が成立する :

\( \begin{aligned} F(a)&< \varepsilon,\\ 1-F(b) &< \varepsilon. \end{aligned} \)

また、有界閉区間上の連続関数は一様連続であるため、 \(F\)は \([a,b]\)上で一様連続であり、ある \(\delta > 0\)が存在して

\( \begin{aligned} \forall x, \forall y, |x-y|<\delta \Rightarrow |F(x)-F(y)| < \varepsilon. \end{aligned}\)

ゆえに, \(N\)を十分大きくとれば, （便宜上　 \(F(- \infty) := 0, \ F(+\infty):=1\)として）次のような点列 \(\{x_k\}_{k=0}^{N}\)を構成することができる:

\(\begin{aligned} &-\infty = x_0 < a=x_1 < \cdots<b=x_{N-1} < x_N = +\infty,\\ &|F(x_{k+1})-F(x_k)| < \varepsilon. \end{aligned} \)

このとき、 任意の \(x\in \mathbb{R}\)に対して、 \(x\in [x_k, x_{k+1}]\)なる \(k\)をとれば、 \(F_n, F\)が単調非減少であることに注意して

\(\begin{aligned} F_n (x) - F(x) &\leq F_n(x_{k+1}) - F(x_k)\\ &= F_n(x_{k+1}) - F(x_{k+1}) + F(x_{k+1}) -F(x_k) \\ &\leq \text{max}_{k} |F_n(x_{k+1}) - F(x_{k+1})| + \varepsilon \end{aligned} \)

以上から

\( \begin{aligned} \sup_{x\in \mathbb{R}}|F(x)-F_n(x)| \leq \text{max}_{k} |F_n(x_{k}) - F(x_{k})| + \varepsilon \end{aligned} \)

となり、両辺の上極限を考えれば結論が得られる。

シュミレーション

ここまでの議論で、サンプルサイズ \(n\)が大きくなった場合に \(P\)値が \(0\)へ収束することを数学的に示すことができました。そこで、実際にその収束が起こっている様子を観察することで、起きている事象を実感してみたいと思います。シュミレーションを行う設定としては以下を想定します。

設定

・母集団分布は一様分布を想定する※
・母平均 \(\mu_0\)について, 下記の両側検定を考える：
・帰無仮説 \(H_o\ :\ \mu_{0} = 0\)
・対立仮説 \(H_1\ :\ \mu_{0} \neq 0\)

この設定で、サンプル数 \(n\) の場合の\(P\)値を以下の方法で可視化します。
※分散既知という仮定から、分散から平均値が算出可能な分布を避けるため、一様分布を採用しています。

可視化方法

1.  母集団分布からn個の標本をランダムにサンプリングする

2.  標本平均が正規分布に従っているという仮定の下、\(P\)値の計算を行う

3.  \(n\) に対して上記1,2を100回繰り返し、\(P\)値の平均値をプロットする

可視化結果

母集団として、以下の3パターンので実験した結果を表示します

・一様分布Ａ：[-1, 1]上の一様分布（平均0、分散1/3：帰無仮説が正しい）

・一様分布Ｂ：[-0.95, 1.05]上の一様分布（平均0.05、分散1/3：対立仮説が正しい）

・一様分布Ｃ：[-0.9, 1.1]上の一様分布（平均0.1、分散1/3：対立仮説が正しい）

・一様分布Ｄ：[-0.8, 1.2]上の一様分布（平均0.2、分散1/3：対立仮説が正しい）

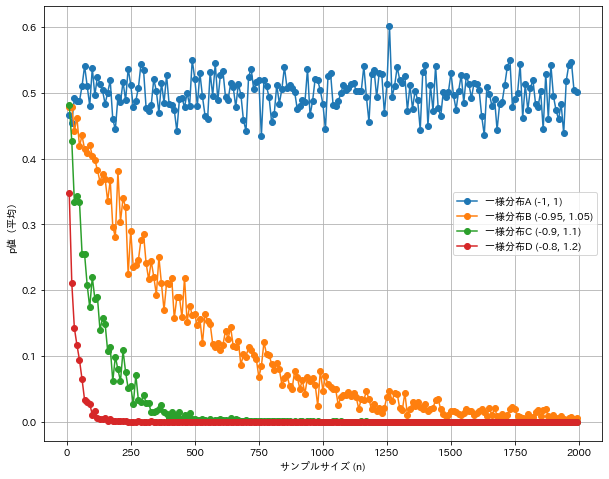
この結果から、以下の情報が読み取れそうです。

・実際に母平均が \(0\)である一様分布においては、サンプル数にかかわらず\(P\)値の値0.5付近で一定である。
・母平均が0でない一様分布では、母平均が0から離れるほどに \(P\)値 は小さく、サンプル数を増加させると0へ収束していく。よって、シュミレーション結果は証明した内容に矛盾しない結果になっていそうです。

まとめ

この記事では、 \(P\) 値 の収束について数学的にどのようにとらえることができるかを考察しました。証明というよりも問題設定を正確に述べる部分に苦労しました。同じような疑問を持った方の理解の一助となれば幸いです。

（参考）実験に用いたコード

#import
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline

#function
def two_sided_test(distribution_func, params, known_variance, sample_size, num_experiments):
    """
    両側検定のシミュレーション関数
    distribution_func: 母集団の分布関数
    params: 分布関数のパラメータ
    known_variance: 既知の分散
    sample_size: サンプル数
    num_experiments: 実験回数
    """
    p_values = []
    for _ in range(num_experiments):
        sample = distribution_func(*params, sample_size)
        z_score = np.mean(sample) / (np.sqrt(known_variance) / np.sqrt(sample_size))
        p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))
        p_values.append(p_value)
    return np.mean(p_values), p_values
    
#config
distributions = {
    '一様分布A (-1, 1)': (np.random.uniform, (-1, 1)),
    '一様分布B (-0.95, 1.05)': (np.random.uniform, (-0.95, 1.05)),
    '一様分布C (-0.9, 1.1)': (np.random.uniform, (-0.9, 1.1)),
    '一様分布D (-0.8, 1.2)': (np.random.uniform, (-0.8, 1.2)),
}
results = {}
sample_sizes = range(10, 2000, 10)
num_experiments = 100
known_variance = 1/3

#caculation
for dist_name, (dist_func, params) in distributions.items():
    p_value_means = []
    for n in sample_sizes:
        mean_p_value, _ = two_sided_test(dist_func, params, known_variance, n, num_experiments)
        p_value_means.append(mean_p_value)
    results[dist_name] = p_value_means

#plot
plt.figure(figsize=(10, 8))

for dist_name, p_value_means in results.items():
    plt.plot(sample_sizes, p_value_means, marker='o', linestyle='-', label=dist_name)

plt.xlabel('サンプルサイズ (n)')
plt.ylabel('p値（平均）')
plt.legend()
plt.grid(True)
plt.show()