はじめに
こんにちは。Customer Analytics Division所属の久保、知野、矢田貝です。データサイエンティストとして、数理最適化技術を用いて電力の需給調整業務を高度化するプロジェクトに携わっております。本記事では、不確実性を考慮した予測・最適化の技術について、電力業界への応用を例に挙げて解説します。
この記事を読んでいる皆さんは、日常生活の中ででんきを使っていることと思います。しかし、その電力がどのように生み出され家庭まで運び届けられているか、背景を詳しくご存知の方は少数派なのではないでしょうか。電力業界には電力を発電する発電事業者、電力を運ぶ送配電事業者、電力を調達し契約者に売る小売事業者をはじめさまざまな関係者がおり、24時間365日、電力システム全体を安定的に稼働させるべく日々尽力されています。特に皆さんが契約を結んでいる事業者は小売事業者といい、皆さん需要家に対して必要十分量の電力を届けられるように市場売買や相対契約などの手段を駆使して電力を調達しています。
そこで本記事では、小売事業者が将来の需要を予測し、電力を調達する需給調整の業務を例に、確率計画法についてご紹介できればと思います。需給調整の前提知識や確率計画法について述べたうえで、簡単な実験も行っております。
需給調整の前提知識
1.小売事業者による計画策定・調達
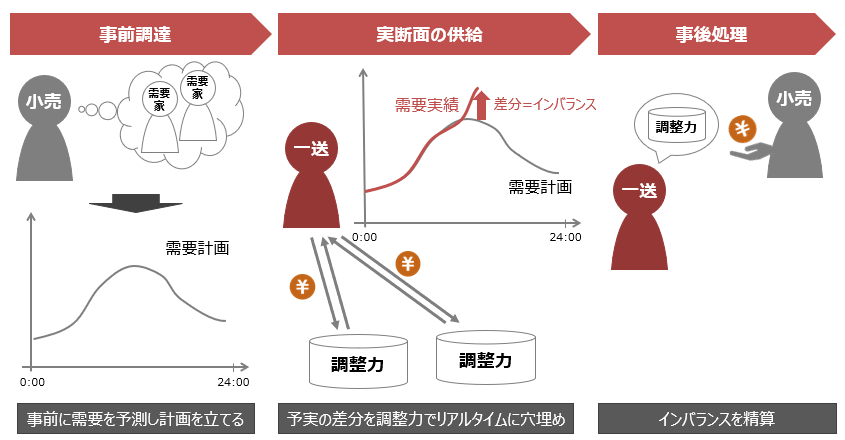
a.小売事業者は実際に電力が使われる前に電力の需要予測などによる見積もりから需要計画を作り、それに合わせて必要な電力(供給力)の調達計画を策定します。
b.この時、小売事業者は需要計画と調達計画を一致させる必要があり、実需給断面の1時間前までに確定させる必要があります。
※同様に、発電事業者も発電計画と販売計画を一致させる必要があり、需給双方が計画を一致させることを計画値同時同量と呼びます[1]。本ブログでは小売事業者のみを想定します。
2.一般送配電事業者による需給調整
a.実需給断面において、一般送配電事業者は事前提出された計画に基づいた送電線の運用(需給調整)を行います。
b.実需要が計画需要に対して過不足になる場合、一般送配電事業者がその過不足を調整します。
3.事後処理
a.調整にかかった費用は事後的に精算され、これをインバランス精算と呼びます。
b.インバランス精算では余った電力は一般送配電事業者に売り、不足した電力は一般送配電事業者から買うという構造になっています。
この前提を元に、「どのように調達を行うのが調達コストを最小に抑えられるのか?」という問題を確率計画法を元に解いていきましょう。…といきたいのですが、1-b, 3-bをそのまま取り込むと確率計画法の枠組みに乗せることができなくなってしまうので、ここでは思考実験的に以下のように改変します。
1-b’:事前調達において、小売事業者は需要量と調達量を一致させる必要はない。ただし、インバランス精算も含めて最終的に一致させる必要はある。
3-b’:電力の余剰・不足は起きないことが望ましいので、いずれに対してもペナルティを付与する。
実際3-b’については、過去にそのような制度をしいていたことがあるようです[1]。
手法の説明
まず、共通する前提条件をいくつか置いておきます。
- 電力調達には様々な手段がありますが、今回は「一日前市場での取引」「自社保有の発電機の稼働」の2つを考えます。
- 需要量については「想定通りシナリオ」「上振れシナリオ」「下振れシナリオ」の3パターンを考えます。それぞれでの需要量やシナリオの生起確率など、詳細な数値は実験パートで述べます。
数の定義
計画策定手法を考えるにあたり必要な数を定義していきます。
■変数
・一日前市場の買電量:\(x_{\rm{mkt}}\in\mathbb{R}, x_{\rm{mkt}}\ge 0 \)
・発電機の稼働有無:\(z_{\rm{gen}}\in\{0, 1\} \)
・余剰インバランス量:\(x_{\rm{imb}}^{+}\in\mathbb{R} \) , 不足インバランス量:\(x_{\rm{imb}}^{-}\in\mathbb{R} \)
└シナリオごとに考える場合は\(x_{\rm{imb}}^+(s), x_{\rm{imb}}^-(s) \) など
■定数
・シナリオ
└シナリオのインデックス:\(s\in\{1, 2, 3\} \)
└シナリオの生起確率:\(p_{s}\in [0, 1], \textstyle\sum_{s}p_{s}=1 \)
・単価
└一日前市場の単価:\(c_{\rm{mkt}} \)
└発電機の稼働コスト:\(c_{\rm{gen}} \)
└インバランスのペナルティ係数:\(\lambda \)
・電力量
└発電機を稼働させた場合の発電量:\(e_{\rm{gen}}\in\mathbb{R}, e_{\rm{gen}}\ge 0 \)
└シナリオ\(s \)の予測需要量:\(\hat{e}_{\rm{dmd}}(s)\in\mathbb{R}, \hat{e}_{\rm{dmd}}(s)\ge 0 \)
└─予測需要量の期待値:\(\bar{e}_{\rm{dmd}} = \textstyle\sum_{s} p_{s} \hat{e}_{\rm{dmd}}(s) \)
確率計画法を用いない手法
需要量の確率的なブレを考慮しない場合では、需要量の期待値を予測し、実際の需要量も期待値に一致すると仮定して計画策定する手法が考えられます。前提3-b’を考慮すると最小化したいのは調達費用とインバランスのペナルティなので、それらの和を目的関数とします。また前提1-b’をもとに、計画した調達量と、需要に対しインバランス精算を加味した量が一致するという制約を置きます。
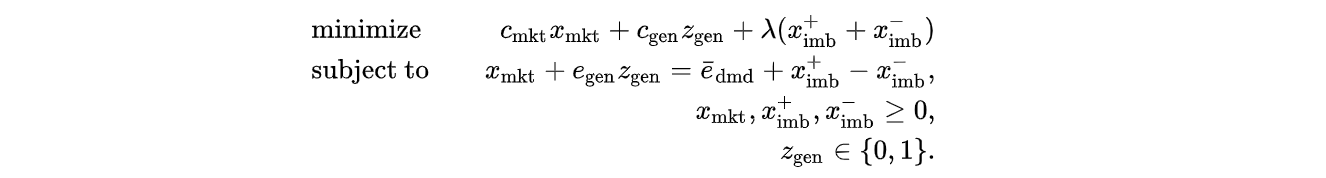
計画策定を混合整数計画問題として定式化することができました。
確率計画法を用いる手法
今回、需要量のシナリオ情報が事前に得られているので、その情報を活用します。改めて、時間の流れを確認してみると以下の通りになります。
■まず、事前に一日前市場の調達量や、発電機の発電量を決める
■その後、需要量が確定する。需要量に応じて、ペナルティが最小になるインバランス量が決定する…※
■最終的に発生するコストは、事前の調達コストと事後のインバランス精算費用の和である
確率計画法の文脈では、不確定な量に対しその前に決定しておくべき変数を1段階変数と呼びます。一方、その量の確定を待ってから決定できる変数を2段階変数と呼びます。この2つを用いて最適化する手法を二段階確率計画法と呼びます[2, 3]。
1段階変数を決める際に将来の2段階変数での見込みペナルティも考慮して最適化をしたいので、最適化問題としては以下のような問題を解くことになります。

1段階変数を決めるときに、仮想的にあるシナリオが実現したと仮定してその状況下で2段階変数の最適化も行ってしまう、という形になります。
これを踏まえ、今回の計画策定を二段階確率計画法として定式化すると以下のようになります。
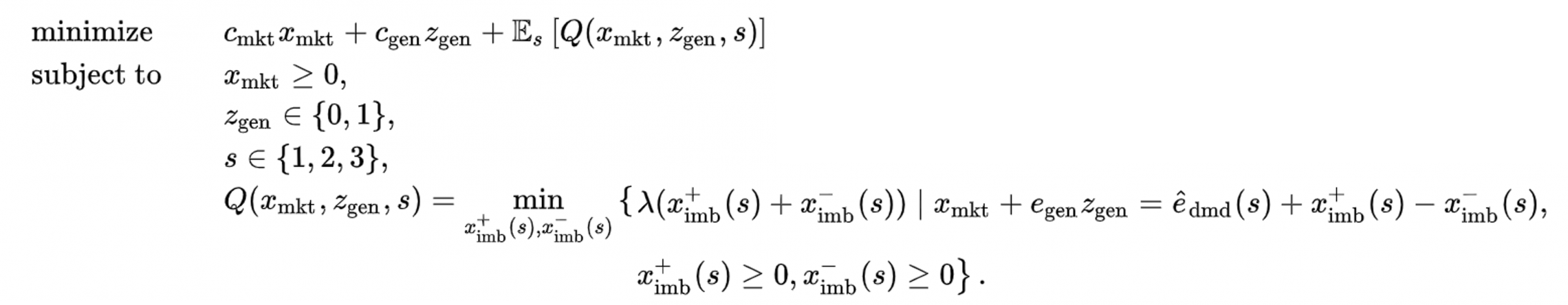
このままだと混合整数計画問題に見かけ上帰着できていないので、次の等価な問題に変換します。
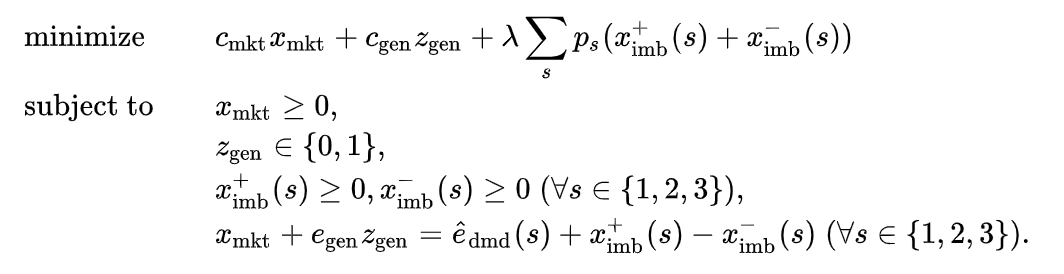
混合整数計画問題として定式化できました。
手法の比較
2つの方法で問題を解いたときに、得られる解の良さを定量的に評価しましょう。二段階確率計画法では、各シナリオごとに2段階変数を実際に最適化した結果を目的関数に含めていました。一方で確率計画法を用いない方法で述べた手法(期待値法と呼びましょう)は各シナリオの情報は考慮していないので、「期待値を使って解は得られたけど、実際その解で各シナリオでどれくらいのコストになるのか?コストの期待値はどの程度か?」は別途算出する必要があります。
期待値法における期待コスト\(\mathrm{EEV} \)は、決定した一段階変数をもとに各シナリオでのコストを求め、それの期待値として算出されます。具体的には、得られた最適解を\(\bar{x}_{\rm{mkt}}(\bar{e}_{\rm{dmd}}), \bar{z}_{\rm{gen}}(\bar{e}_{\rm{dmd}}) \)と置いたときに
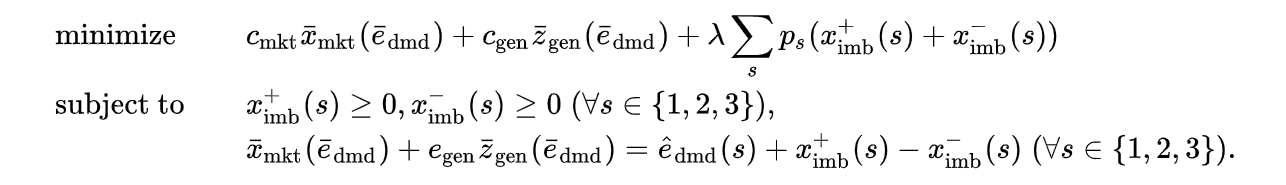
の最適値として得られます。二段階確率計画法と同様に各シナリオでインバランス量を最適化しますが、一日前市場の調達量や発電機発電量は固定します。
他方、二段階確率計画法の期待コスト\(\mathrm{RP} \)は目的関数値そのものの値となります。これを用いて、2つの手法の期待コストの差異\(\mathrm{EEV}-\mathrm{RP} \)を見ることでどちらがどれくらいコスト優位かを見ることができます。この差異はVSS (value of stochastic solution)と呼ばれています。
実験設定
さて、二段階確率法を導入する意義を、数値実験を通じて確認してみましょう。上記で定義したVSSを算出するため、実験の数値を設定します。
まず、シナリオによらず確定的な定数、すなわち一日前市場の単価、発電機を稼働させた場合の発電量、発電機稼働コストを以下のように設定します。

次に、確率によって上振れ・下振れが想定される予測需要量とその生起確率を、以下のように設定します。1が「想定通りシナリオ」、2が「上振れシナリオ」、3が「下振れシナリオ」です。
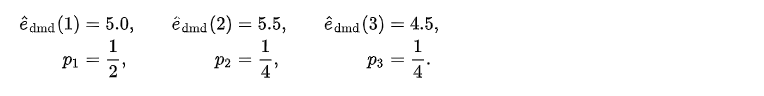
ここで、予測需要量の期待値\(\bar{e}_{\mathrm{dmd}}=5.0 \)はとなります。最後にインバランスのペナルティ係数は、一日前市場の単価および発電機稼働コストとの大小関係を考慮し、10以上50以下の範囲内で0.8刻みで変化させ、VSSとの関係を確認します。
実験結果
インバランスのペナルティ係数\(\lambda \)を変化させながらVSSの値を算出したところ以下のような結果が得られました。
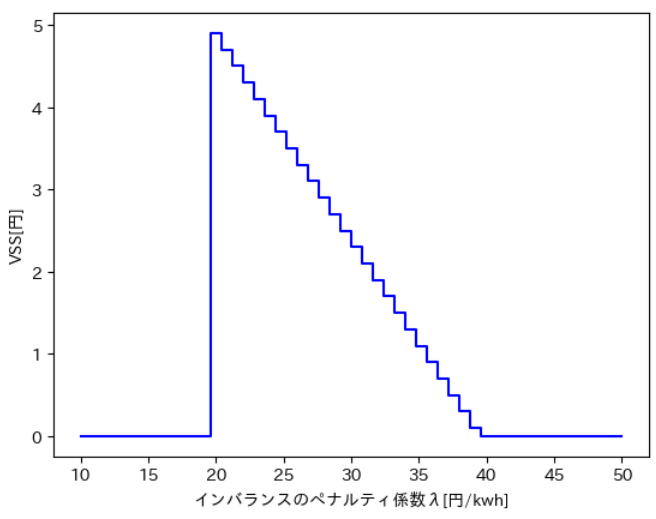
ペナルティ係数λごとに算出したVSS
どのペナルティ係数の値でもVSS≧0であることが確認できるので、二段階確率計画法は期待値法に劣らないという結果が得られました。実はVSSは一般に非負であることが理論的に証明でき[2]、今回の実験もそれを肯定的に確認できる結果となりました。
VSSの細かい挙動の解釈については、下記の通りになります。
■ペナルティ係数\(\lambda \)が20以上40以下の値ではVSSが正の値を取っています。このケースでは、二段階確率計画法が期待値法よりコストの観点で優れていると言えます。
■一方、ペナルティ係数\(\lambda \)の小さいところと大きいところではVSSは0になっています。これは期待値法と二段階確率計画法で得られる解\(x_{\rm{mkt}}, z_{\rm{gen}} \)が等しいことによります。この振る舞いは以下のように代数的に理解することができます。
・ペナルティ係数\(\lambda \)が一日前市場の単価\(c_{\rm{mkt}}=20 \)より小さいとき
└どちらの手法でも、一日前市場での買電による目的関数の上昇を抑えるために、\(x_{\rm{mkt}}=0 \)の解が得られます。発電機の発電量\(z_{\rm{gen}} \)についても、2つの手法で解が同じことが言えます。そのためVSSは常に0となります。
・ペナルティ係数が一日前市場の単価\(c_{\rm{mkt}}=20 \)より十分大きいとき
└目的関数の中でも、インバランスのペナルティ項が重大視されます。
└期待値法では\(x_{\rm{imb}}^+, x_{\rm{imb}}^-=0 \)、すなわち一日前市場での調達と発電機のみで需要を満たす\(x_{\rm{mkt}}+e_{\rm{gen}}z_{\rm{gen}}=\bar{e}_{\rm{dmd}} \)の解が得られ、インバランスのペナルティは0となります。
└二段階確率計画法では、補遺の議論により(\(\mathrm{Med}[E_{\rm{dmd}}] \)が一意に存在するときには)\(x_{\rm{mkt}}+e_{\rm{gen}}z_{\rm{gen}}=\mathrm{Med}[E_{\rm{dmd}}] \)を満たす解が得られます。ここで、確率変数\(X \)に対し\(\mathrm{Med}[X] \)は確率変数\(X \)の中央値を表し、\(E_{\rm{dmd}} \)は需要量の確率変数です。
└従って、\(\mathbb{E}[E_{\rm{dmd}}]=\mathrm{Med}[E_{\rm{dmd}}] \)の場合は2つの手法の解が等しいためVSSは0になり、一方\(\mathbb{E}[E_{\rm{dmd}}]\neq\mathrm{Med}[E_{\rm{dmd}}] \)の場合はVSSは正になります。今回は\(\mathbb{E}[E_{\rm{dmd}}]=\mathrm{Med}[E_{\rm{dmd}}]=5.0 \)と前者の式を満たす設定だったため、VSSは0となりました。
まとめと展望
電力需給調整の業務を例に、確率計画法における期待値法と二段階確率計画法を用いた最適化問題を定式化しました。また、簡単な実験インスタンスにおいてVSSを確認することで、二段階確率計画法が期待値法に比べ予測のブレを考慮することでよりコストを削減できる手法であることを確認しました。
昨今DXの推進が叫ばれる中、数理最適化と相性の良い業界では実務適用が進められているものと思います。特に未来に関する意思決定の場では単一の予測が信頼しきれないケースも多分にあるため、このような不確実性にどのように対処していくべきかという論点は無視できないのではないのでしょうか。そのような問題に向き合う最初の一歩として、本記事で理解を深めていただければ喜ばしい限りです。
ARISE analyticsでは数理最適化をはじめとしたデータ分析・AI技術を用いたDX支援を行っています。弊社の取り組みに興味を持っていただいた方はぜひお声がけください。
https://www.ariseanalytics.com/contact/
参考文献
[1] 2021年度以降のインバランス料金の詳細設計等について. 第37回制度設計専門会合事務局提出資料, 2019.
[2] 椎名孝之. 確率計画法. 朝倉書店, 2015.
[3] 高野祐一. 確率計画法の理論と応用. 専修ネットワーク&インフォメーション, 23 (2015), pp. 15–22.
補遺
二段階確率計画法の場合において、\(\lambda \)が十分大きい場合に最適解が\(x_{\rm{mkt}}+e_{\rm{gen}}z_{\rm{gen}}=\mathrm{Med}[E_{\rm{dmd}}] \)を満たすことを簡略的に証明します。\(E_{\rm{dmd}} \)が離散確率分布であり、中央値が一意に存在することを前提として議論を進めます。
\(\lambda \)が十分大きいため目的関数の一部の項を無視することで、\(\lambda(x_{\rm{imb}}^++x_{\rm{imb}}^-) \)が目的関数であると見なせます。ここで、(証明は省きますが)最適解では\(x_{\rm{imb}}^+, x_{\rm{imb}}^- \)のいずれかは0に等しいという事実を用いれば\(x_{\rm{imb}}^++x_{\rm{imb}}^-=|x_{\rm{imb}}^+-x_{\rm{imb}}^-| \)と書けます。等号制約を代入することで目的関数は結局\(\lambda\mathbb{E}[|E_{\rm{dmd}}-x_{\rm{mkt}}-e_{\rm{gen}}z_{\rm{gen}}|] \)と変形することができます。一般に確率変数\(X \)に対し任意の実数\(c \)について平均絶対誤差\(\mathbb{E}[|X-c|] \)が存在する場合、\(\arg\min_{c}\mathbb{E}[|X-c|] \)は確率変数\(X \)の中央値\(\mathrm{Med}[X] \)に等しいことが示せます。\(E_{\rm{dmd}}\ge 0 \)であり\(x_{\rm{mkt}}+e_{\rm{gen}}z_{\rm{gen}} \)は0以上の任意の値を取れるため、\(x_{\rm{mkt}}+e_{\rm{gen}}z_{\rm{gen}}=\mathrm{Med}[E_{\rm{dmd}}] \) が最適解で満たされます。目的関数の一部の項を無視できたという前提で当初の主張を言えました。
より厳密には、\(E_{\rm{dmd}} \)が離散確率分布であり中央値が一意に存在することを利用します。\(\frac{1}{\lambda}=\tau \)と変換した上で最適解が\(0 \le \tau \ll 1 \)において一定なことを示すことで、\(\tau=0 \)の場合(目的関数の一部の項を無視した場合)と同様に\(0<\tau\ll 1 \)でも成り立つことが示せます。



